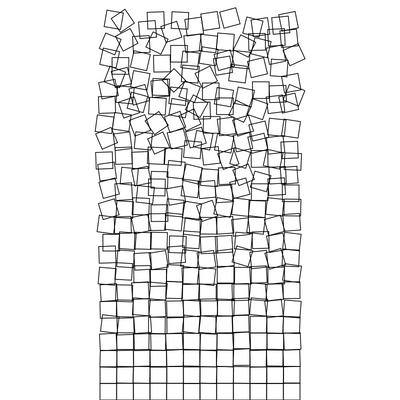
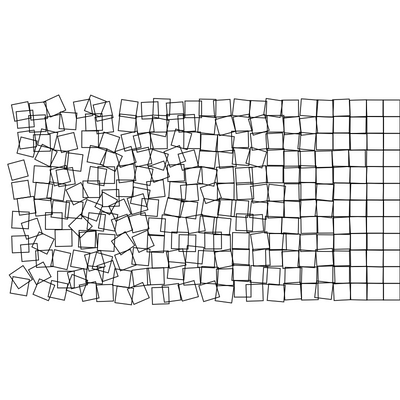
Recréer un classique de l'art généré par ordinateur avec p5js.

Bluez

, Jan.24

'Schotter', Georg Nees (1968)

Histoire

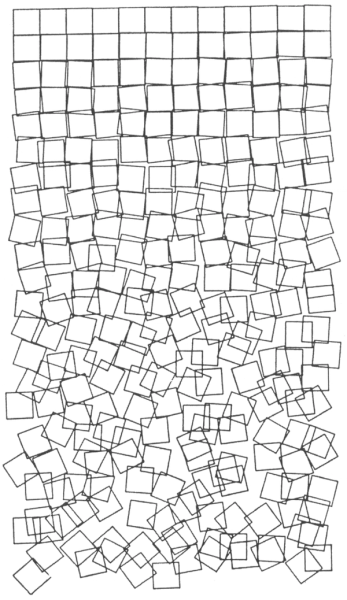
Georg Nees fut pionnier dans le domaine de l'art généré par ordinateur. Alors qu'il travaillait pour Siemens, il prit l’initiative d'utiliser le traceur industriel Zuse Z64 pour créer "quelque chose d'inutile [sic]", initiant une longue tradition encore en vigueur, d'ingénieurs faisant assumer à leur entreprise la charge financière de leur passe-temps.

Zuse Z64 "Da Baby"

Lors de l'exposition ComputerGraphik de 1965 et des années qui suivirent, il présenta des oeuvres révolutionnaires, telles que Schotter (1968), que nous allons recréer ici.

Du chaos seul, l'ordre peut naître. Et vice versa.

Pre-requis

Afin d'éviter des calculs de coordonnées laborieux, nous utiliserons les méthodes p5js suivantes:

rectMode
translate
push/pop
randomGaussian

Plutôt que de calculer les coordonnées de chaque carrés, ce qui produirait un code peu lisible, nous allons voir comment utiliser les fonctions push/pop et effectuer des transformations.

Algorithme

Créer une grille, en suivant les étapes suivantes:

dessiner N carrés horizontalement dans une largeur donnée
déplacer le pointeur vers le bas de l'écran, de la hauteur d'un carré
retour à l'étape 1. jusqu'à ce que le bas de l'écran soit atteint

On applique avant de dessiner chaque carré, en plus de la transformation de base, une transformation aléatoire proportionnelle à la position verticale du carrée dans l'écran.

En appelant au préalable rectMode(CENTER), les transformations seront visibles depuis le centre des carrés, plutôt que depuis le coin en haut à gauche, comme c'est le cas par défaut. On applique également une translation pour faire en sorte qu'ils soient tous tracés dans les limites de l'écran.

Ordre

Commençons par initialiser notre canvas, rectMode et la couleur de fond.

function setup() {
  createCanvas(800, 800);
  rectMode(CENTER);
  background(255);
}

et dessinons une série de carrés occupant toute la largeur.

function setup() {
  createCanvas(800, 800);
  rectMode(CENTER);
  
  background(255);
  
  const resX = 12; // number of squares per line
  const w = width / resX; // dimension of a square
  
  translate(w * 0.5, w * 0.5); // offset by half a square
  
  for (let i = 0; i < resX; i++) {
    square(0, 0, w);
    translate(w, 0);
  }
}

A line of squares.

Remarquons que dessiner un carré à la position (0, 0) après avoir appelé translate produit bien un carré à la bonne position: le point de référence auquel nous dessinons est déplacé vers la droite d'une largeur de carré, à chaque itération...

Afin de dessiner une nouvelle ligne de carrés au dessous de la première, ce point de référence doit être remis à sa valeur précédente. Pour cela, nous allons utiliser les méthodes push et pop.

Entourons le code précédent d'une nouvelle boucle, et appliquons une nouvelle transformation, verticale cette fois.

...
for (let j = 0; j < 2; j++) {
  push();
  
  for (let i = 0; i < resX; i++) {
    square(0, 0, w);
    translate(w, 0);
  }
  
  pop();
  translate(0, w);
}
...

appeler push stocke l'état initial de la transformation
des transformations sont appliquées
appeler pop remet le point de référence à son état précédent

L'appel à translate dans la boucle extérieure, bouge le point de référence d'un carré vers le bas. Toutes les transformations ultérieures sont appliquées depuis cette position.

Afin de couvrir tout l'écran de carrés, utilisons une boucle while dont nous sortirons lorsque le bas de l'écran sera atteint.

...
let y = 0;

while (y + w < height) {
  push();
  
  for (let i = 0; i < resX; i++) {
    square(0, 0, w);
    translate(w, 0);
  }
  
  pop();
  translate(0, w);
  
  y += w;
}
...

Notre grille est prête à être bousculée. 🙂

Chaos

Plutôt que la méthode random, nous utiliserons randomGaussian qui génèrent des nombres aléatoires suivant une distribution normale, que nous pourrons régler finement plus tard... Le premier argument est la valeur autour de laquelle les nombres sont centrés; le second argument est la déviation par rapport à cette valeur.

Horizontalement, d'abord.

...
const d = y / height;

for (let i = 0; i < resX; i++) {
  const dX = d * randomGaussian(0, 0.3);
  
  push();
  translate(dX * w, 0);
  square(0, 0, w);
  pop();
  
  translate(w, 0);
}
...

On stocke le point de référence avec push, on déplace le pointeur d'une valeur aléatoire, on dessine notre carré, pour finalement retourner à la position initiale.

Cette valeur est proportionnelle à la position verticale du carré dans l'écran.

Appliquons le même principe pour la coordonnée Y et la rotation:

...
const d = y / height;

for (let i = 0; i < resX; i++) {
  const dX = d * randomGaussian(0, 0.1);
  const dY = d * randomGaussian(0, 0.1);
  const dR = d * randomGaussian(0, 0.2);
  
  push();
  translate(dX * w, dY * w);
  rotate(dR * QUARTER_PI);
  square(0, 0, w);
  pop();
  
  translate(w, 0);
}
...

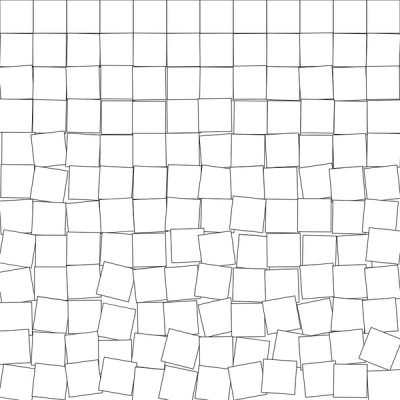
On se rapproche!

Ajoutons des marges, enlevons le remplissage de couleur, et réglons l'aléatoire...

function setup() {
  createCanvas(800, 800);
  rectMode(CENTER);

  background(255);
  noFill();
  strokeWeight(1.5);

  const resX = 12;
  const margin = width * 0.25;
  const w = (width - margin * 2) / resX;

  translate(margin + w * 0.5, w * 0.5);

  let y = 0;

  while (y + w < height) {
    const d = y / height;
    push();

    for (let i = 0; i < resX; i++) {
      const dX = d * randomGaussian(0, 0.2);
      const dY = d * randomGaussian(0, 0.3);
      const dR = d * randomGaussian(0, 0.4);

      push();
      translate(dX * w, dY * w);
      rotate(dR * QUARTER_PI);
      square(0, 0, w);
      pop();

      translate(w, 0);
    }

    pop();
    translate(0, w);

    y += w;
  }
}

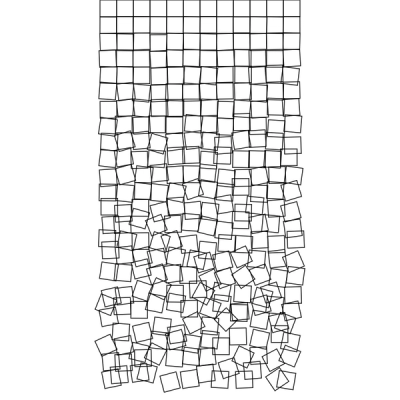
Conclusion

Schotter est formidable à la fois par sa simplicité et son propos. Une chose remarquable est qu'en changeant son orientation, son sens s'en trouve également changé.